
Regletas Montessori o Cuisenaire: cómo usarlas + Imprimible

Las regletas Montessori son el material en madera que corresponde en número y color a las barras de perlas Montessori. Las regletas en madera permiten establecer ciertas relaciones de una forma más geométrica que con las perlas permitiendo actividades diferentes. Se complementa con el material cúbico para conceptos más avanzados como las raíces cúbicas.


En este post os enseñaremos algunas actividades y demostraciones manipulativas de conceptos matemáticos para realizar con las regletas Montessori pero también con las regletas Cuisenaire, ya que solamente cambian los colores.
Las regletas, independientemente de sus colores, son un material fantástico para la manipulación que ofrece la posibilidad de construir y descubrir conceptos a través de ellas. Son ideales para plantear retos que los niños pueden resolver generando conceptos matemáticos por sí solos, de esta forma el grado de comprensión de los conceptos, propiedades y relaciones entre números es mucho más profundo. Es mucho más recomendable plantear desafíos a los niños que les permitan descubrir por ellos mismos que presentarles los conceptos directamente, es por ello que las actividades descritas a continuación están encaradas a que los adultos sepamos cómo llevar a cabo los conceptos matemáticos con las regletas, pero lo ideal sería que a la hora de presentarlas a los niños les demos las pautas para ayudarles a investigar por ellos mismos, ya que las regletas deberían ser el medio por el que lleguemos al aprendizaje, no el fin en sí mismas.

Experimentación libre

En los primeros contactos de los niños con las regletas debemos dejar que experimenten de forma libre con ellas. De esta forma irán conociendo el material con sus características de forma natural. Por sí solos irán reconociendo los colores y las longitudes de cada una de las regletas.
Cada regleta corresponde a un número y para comprobarlo podemos ver cuántos cuadritos de uno corresponden con cada regleta. Así podremos ver que la regleta violeta es el número 6.

En estos primeros contactos con las regletas podremos ver las relaciones que hay entre ellas y descubrir muchas curiosidades numéricas.

Comparación de números
Con las regletas es muy visual la comparación de números debido a que cada uno tiene una longitud diferente proporcional. Para la comparación de números podemos usar los símbolos de mayor y menor.

Para comparar las cantidades solo debemos poner una regleta debajo de la otra para ver cuál es menor.

La caja de números y signos aritméticos nos ayudará a establecer estas relaciones y escribirlas de forma manipulativa cuando lleguemos a determinadas conclusiones. Es importante expresar verbalmente aquellas conclusiones a las que vayamos llegando y finalmente expresarlas de forma escrita, ya sea de forma manipulativa con los signos y números o escribiéndolo.


Para números más grandes las tarjetas de madera nos ofrecen una mejor visión del valor posicional de los números.

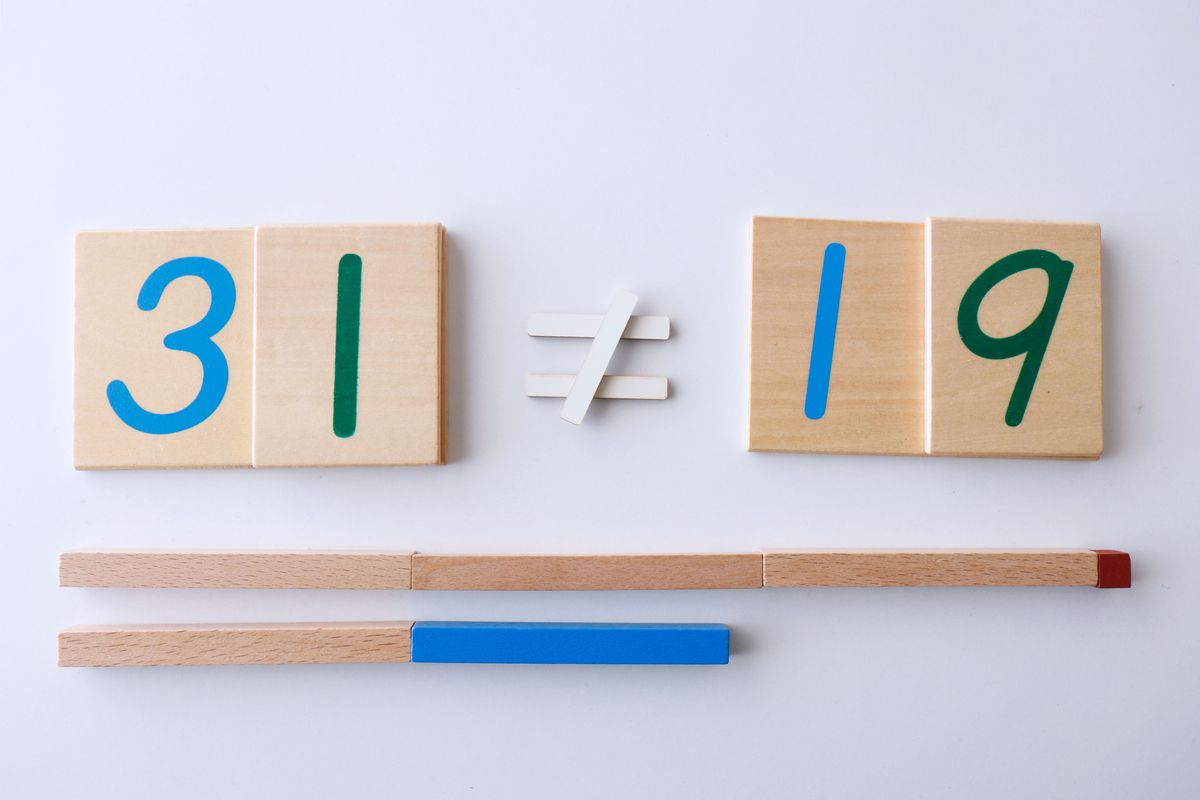
Cada tarjeta tiene un tamaño diferente dependiendo de si son unidades, decenas, centenas o millares. A la hora de construir los números tapamos los ceros dejando ver el valor posicional de cada uno.
Suma
Para sumar dos regletas las pondremos una al lado de la otra, de esta forma es muy visual ver cómo aumenta la cantidad en la suma.


Empezaremos con sumas de dos dígitos pero podemos hacerlo con 3 o más.

Si el resultado es mayor de 10 representaremos el resultado con el menor número de regletas posible.
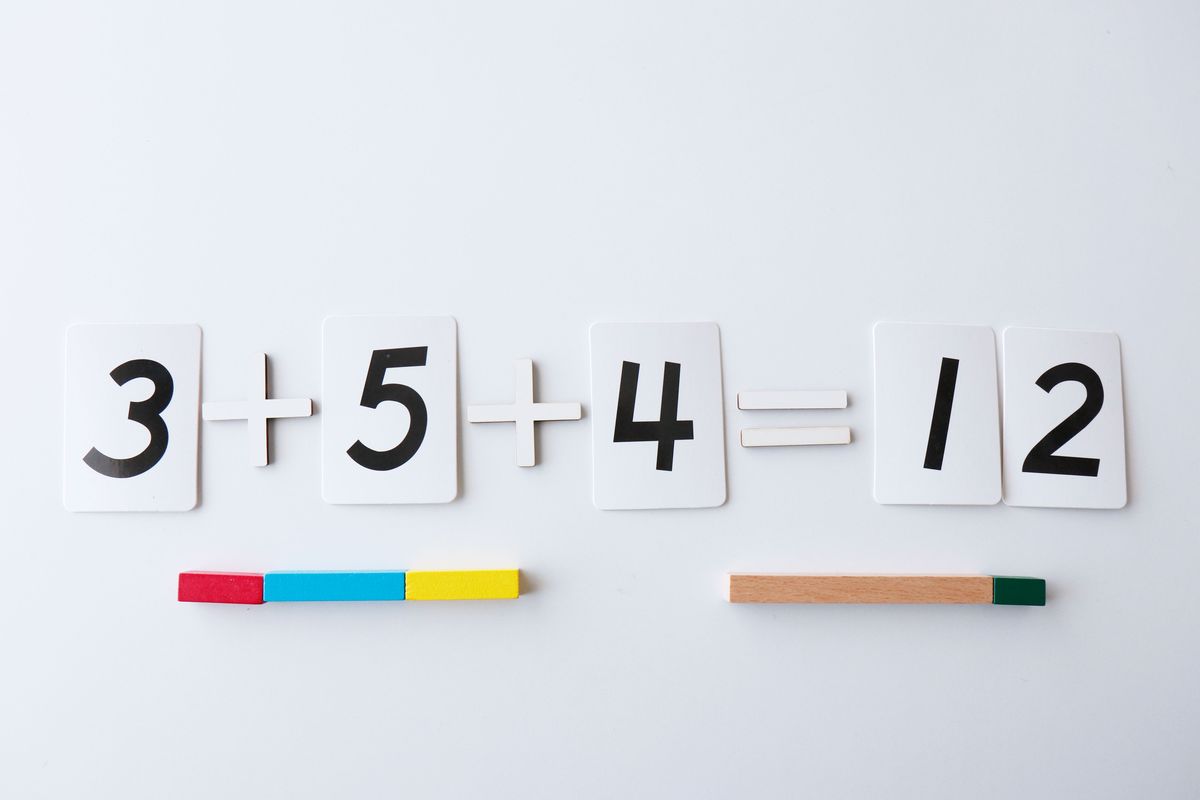
Descubrir uno de los sumandos
Podemos pedir al niño si puede descubrir uno de los sumandos.
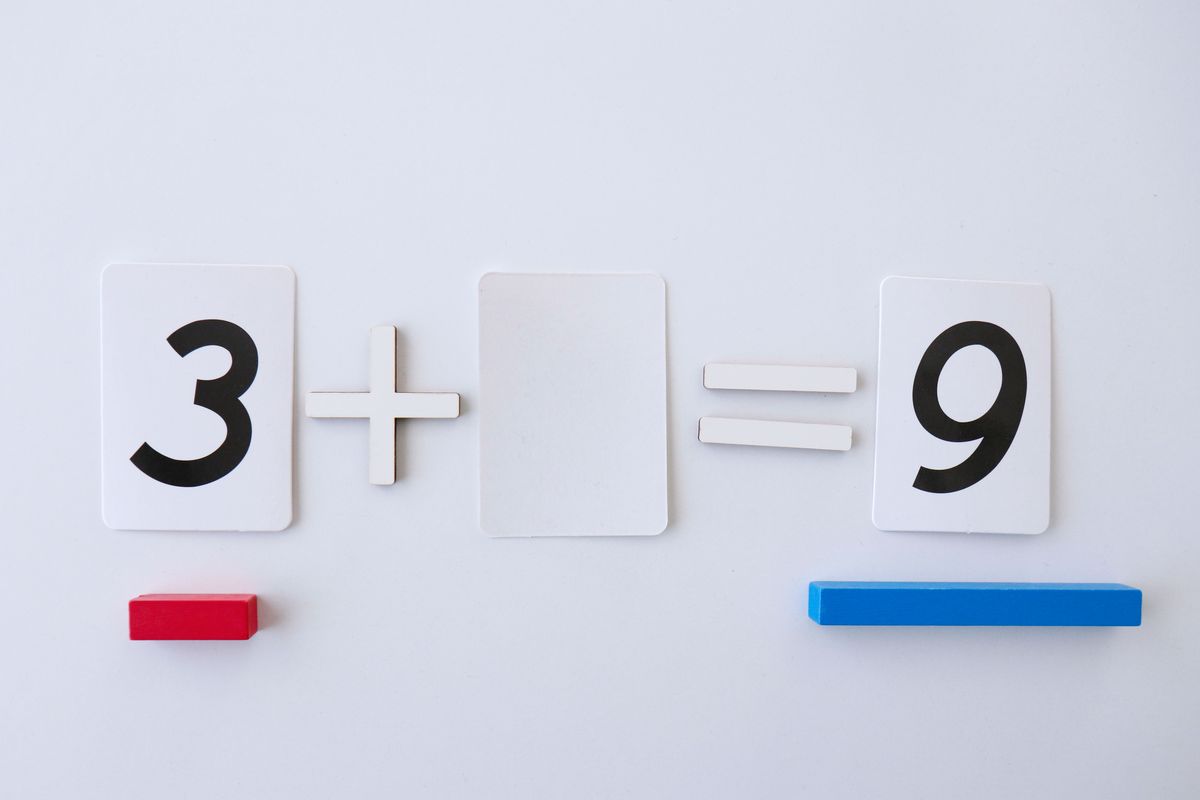
Si situamos una regleta encima de la otra de forma alineada, podemos ver cuál es el número que falta. De esta forma estaremos haciendo una resta de forma indirecta, así pueden descubrir la suma y la resta como operación inversa la una de la otra.
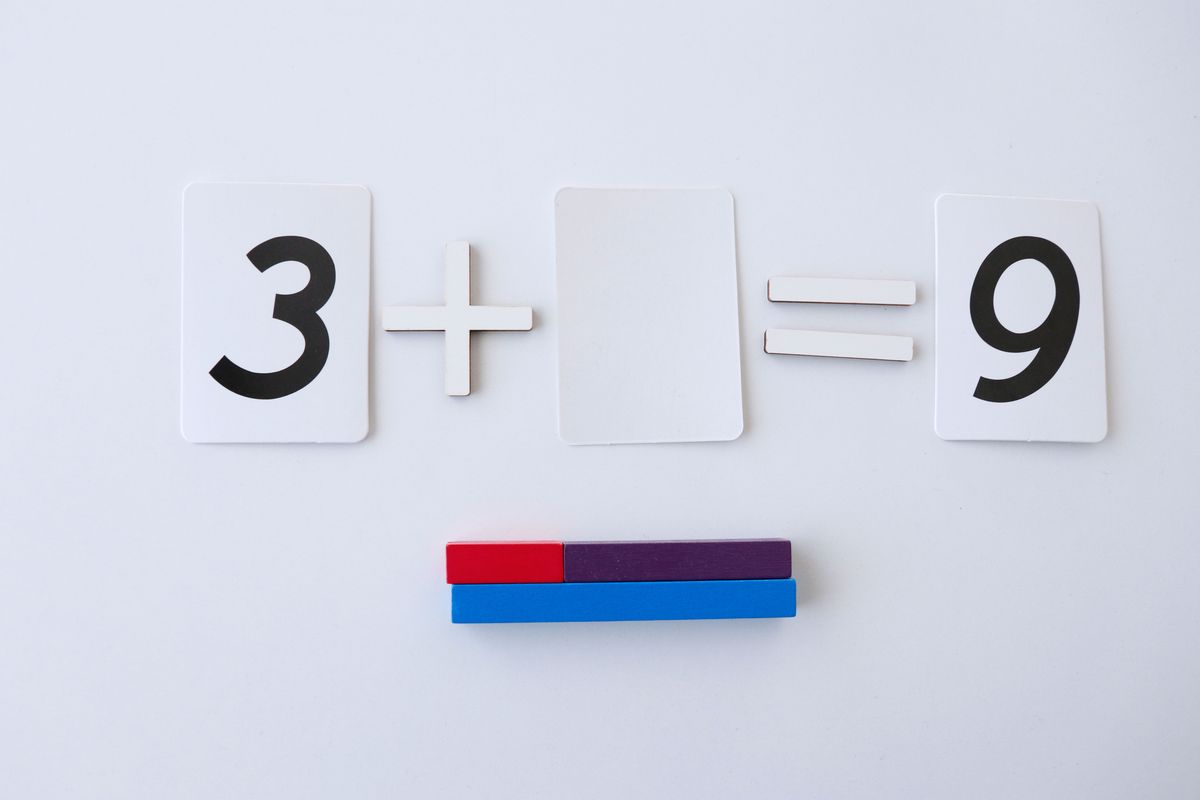
Si usamos las tarjetas de números podremos autocorregirnos girando la tarjeta.

Propiedades de la Suma
Propiedad conmutativa
El resultado de una suma no varía al intercambiar de posición sus sumandos.


Propiedad asociativa
Para sumar más de dos sumandos podemos agruparlos de la forma que queramos que el resultado no se verá afectado.
Por ejemplo, para sumar 5+2+6 podemos hacerlo de diferentes formas.
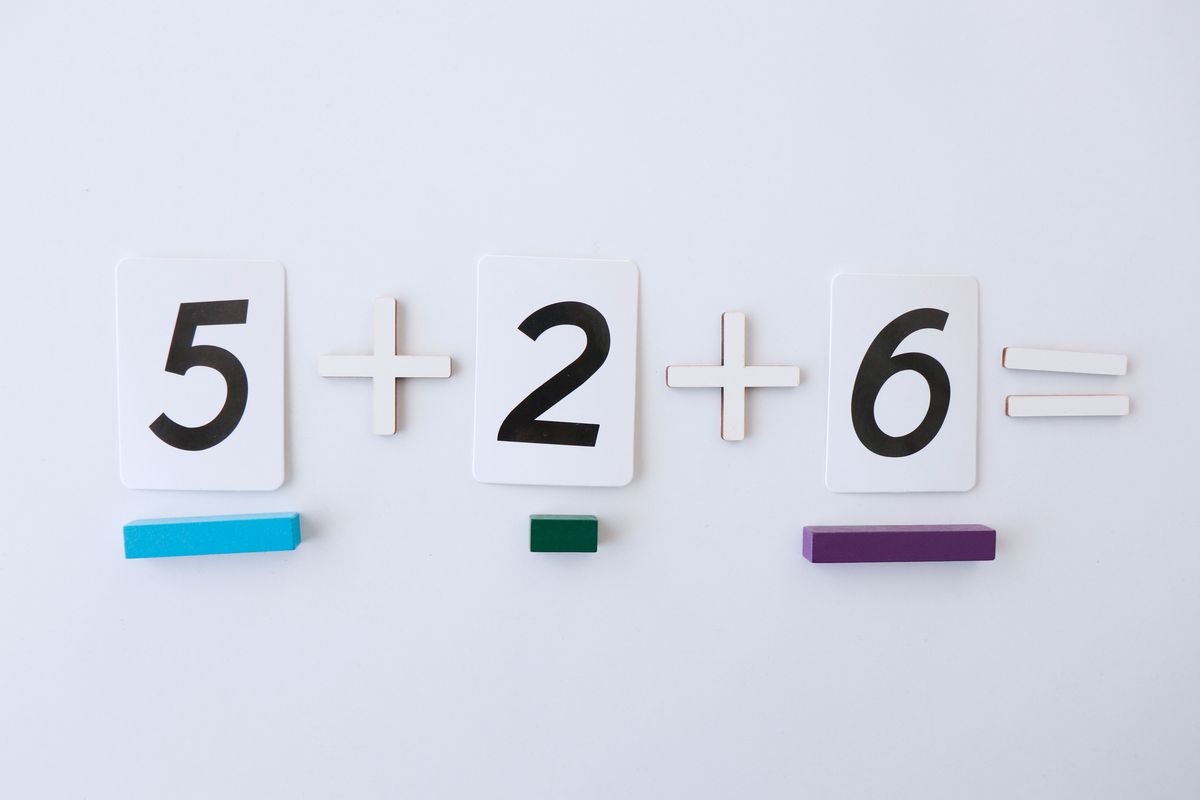
Podemos agrupar los dos primeros sumandos, el 5+2 primero y luego a este resultado sumarle el 6.
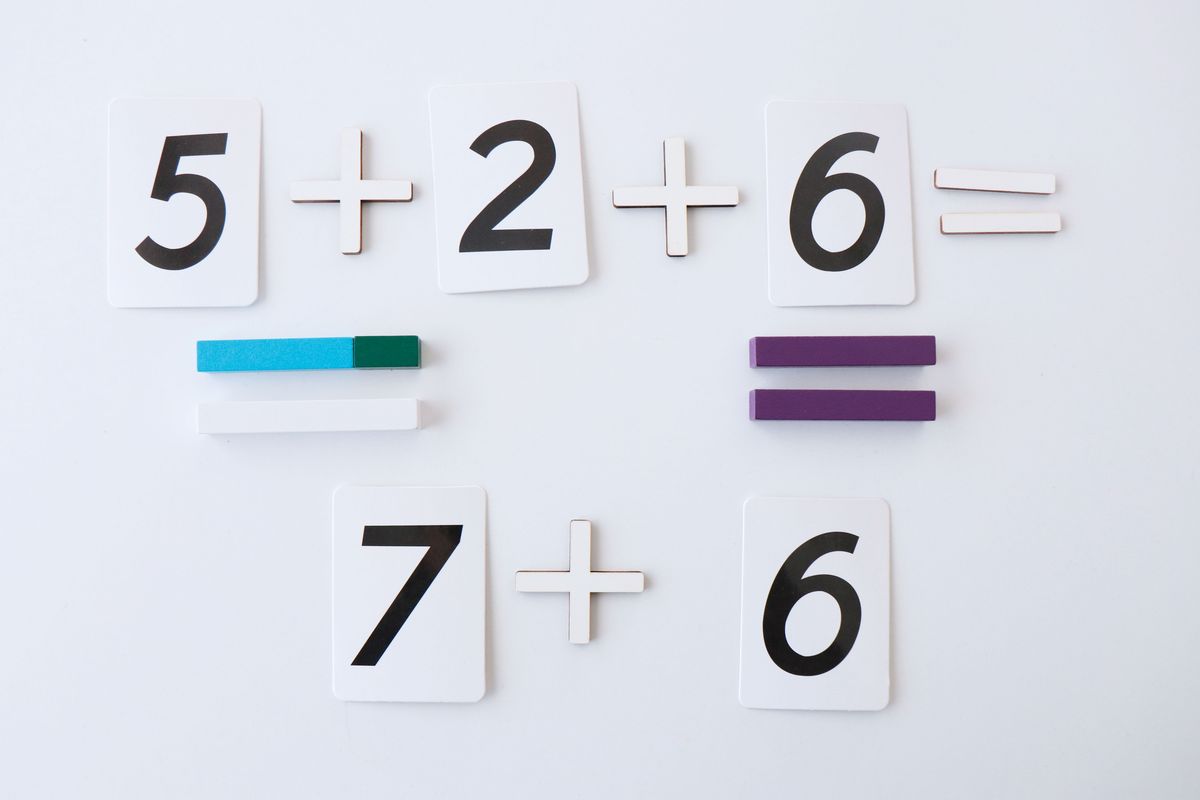
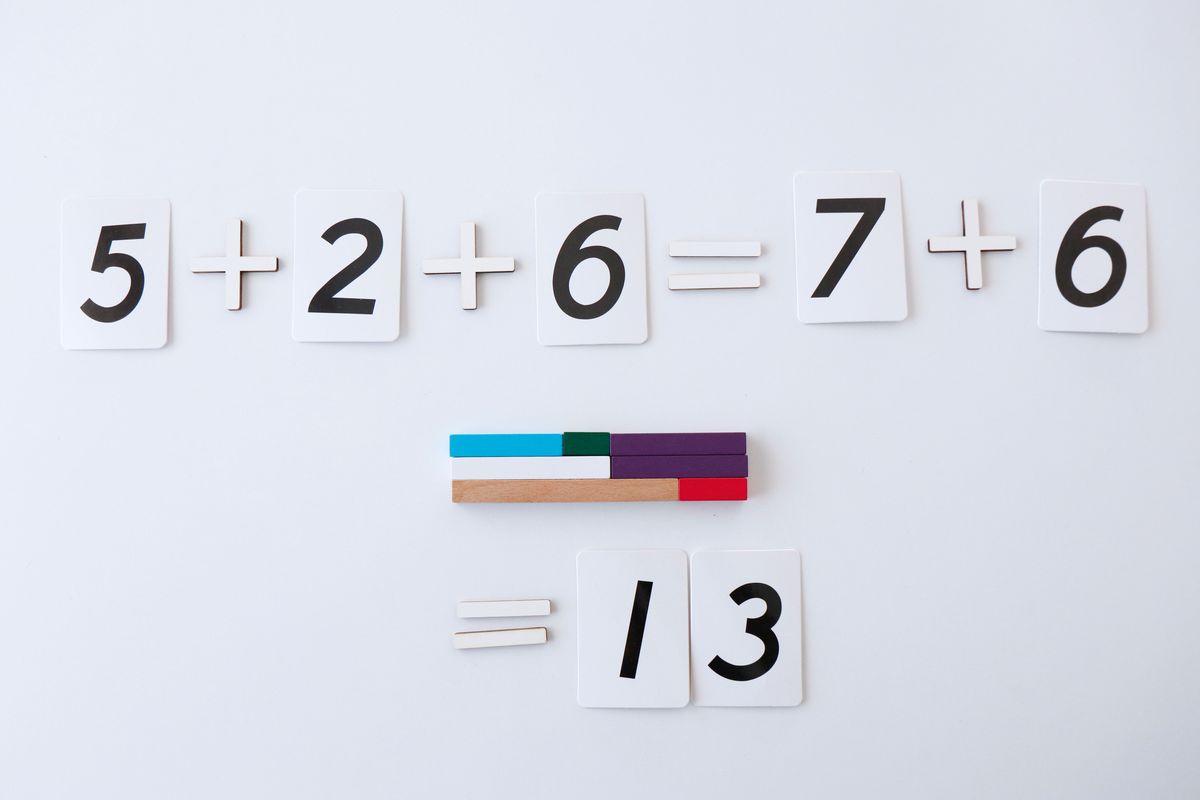
O tal vez prefiramos agrupar los dos últimos sumandos, el 6+2 y luego añadirle el 5.
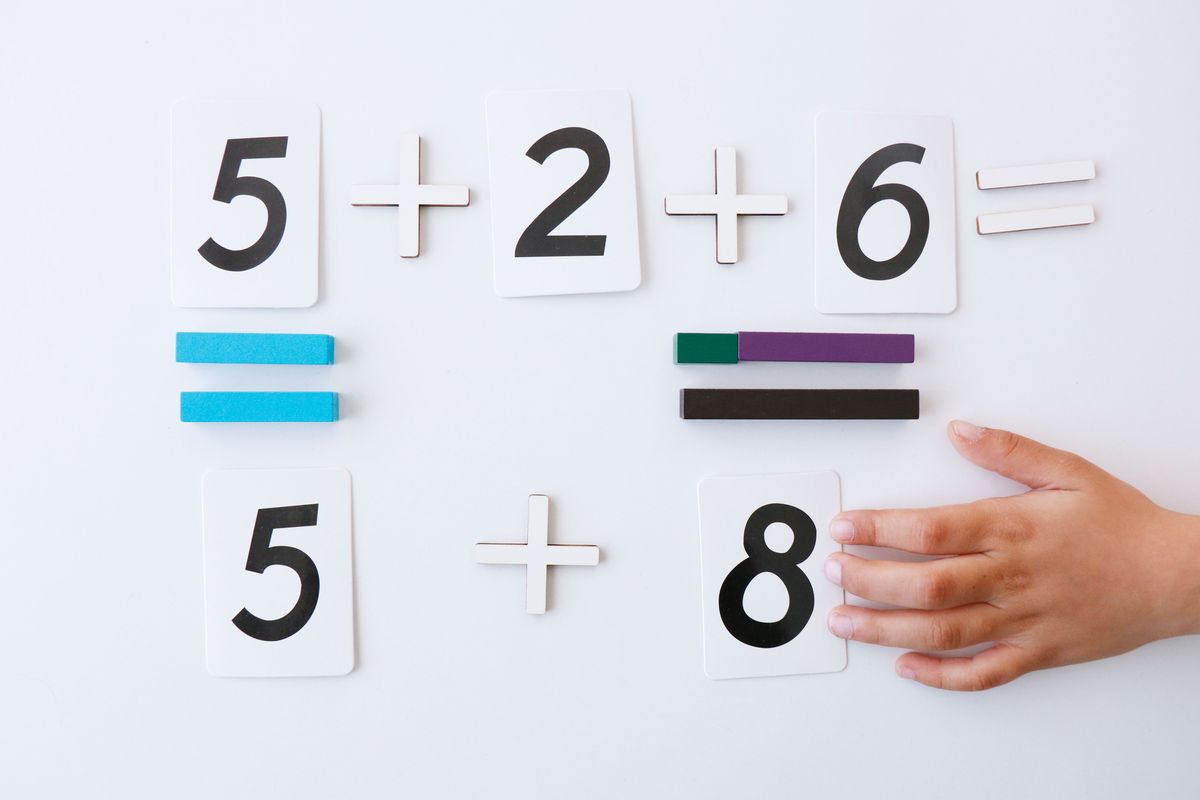
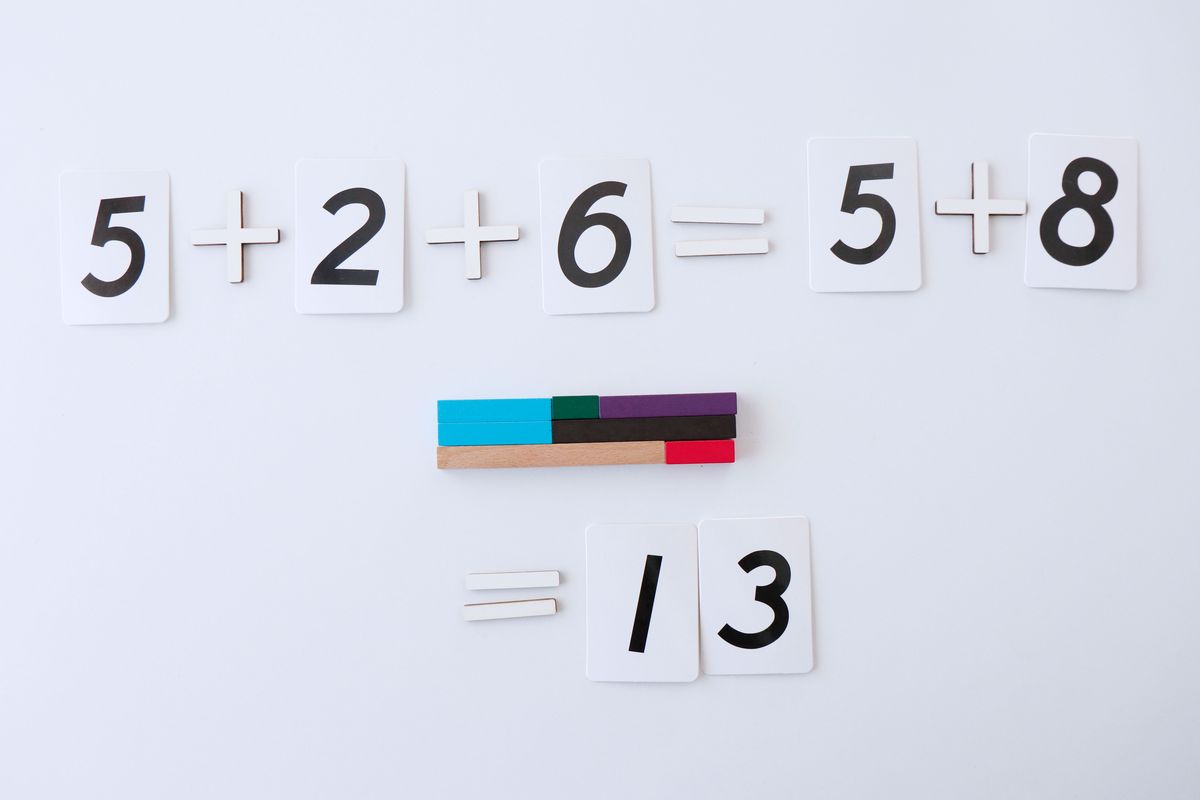
De esta forma podemos llegar también a la conclusión que un número puede descomponerse de varias formas diferentes.
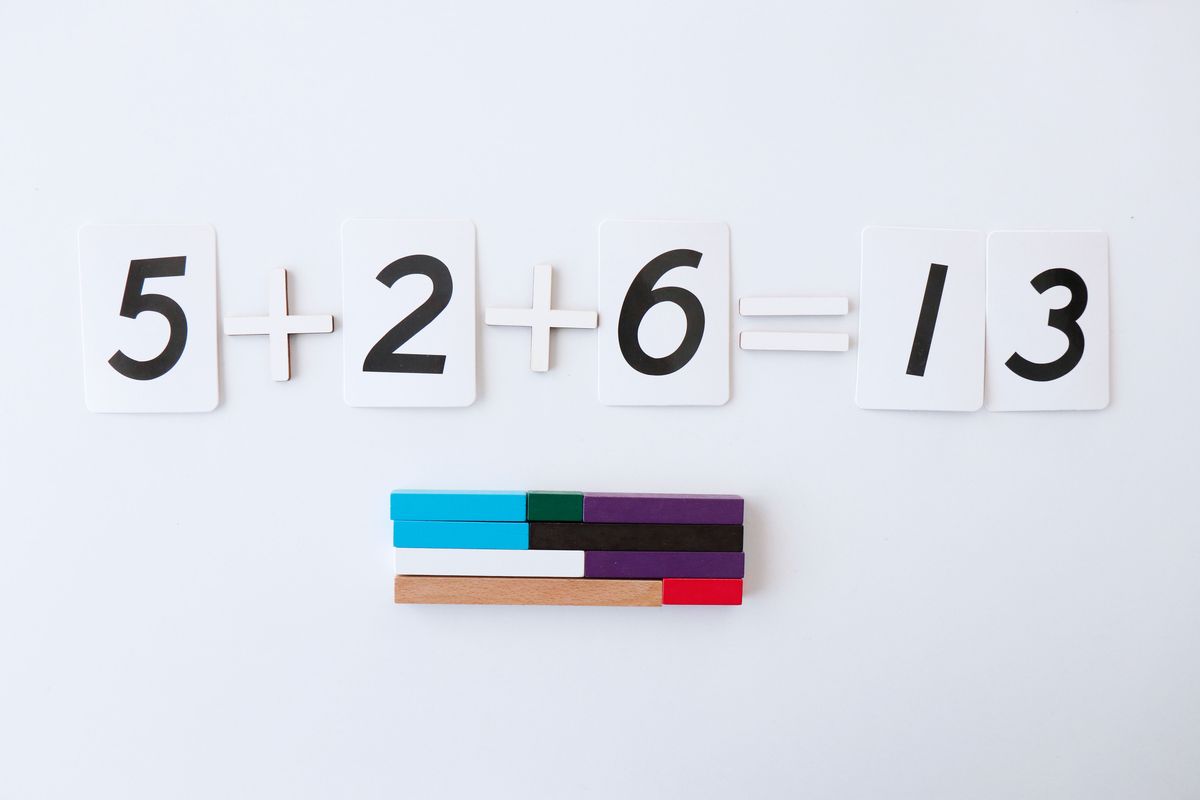
Y por tanto habrá varias sumas diferentes que nos darán el mismo número de resultado. Esto nos llevará también a la descomposición de números.

Resta
Para restar dos números pondremos las regletas una encima de la otra y buscaremos el número que le falta al más pequeño para llegar al más grande.


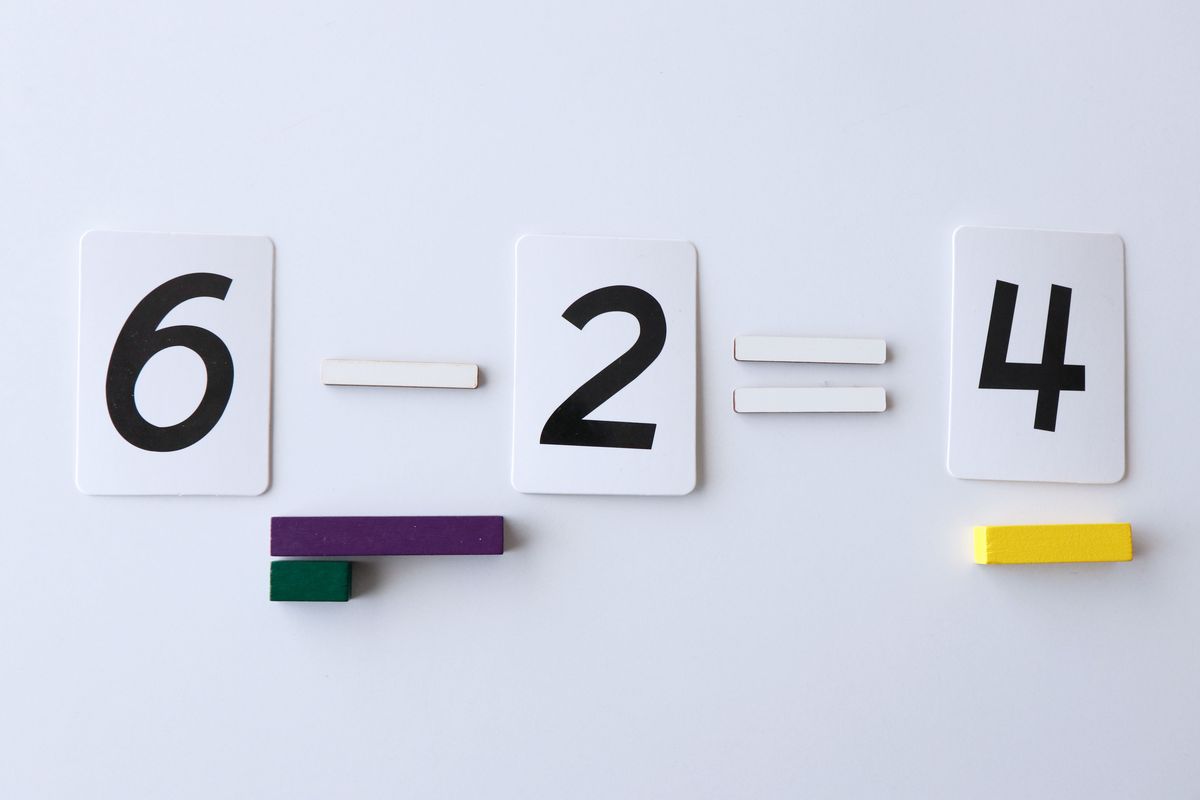
Restas con el mismo resultado
Podemos comprobar que hay varias restas que nos darán el mismo número de forma diferente.
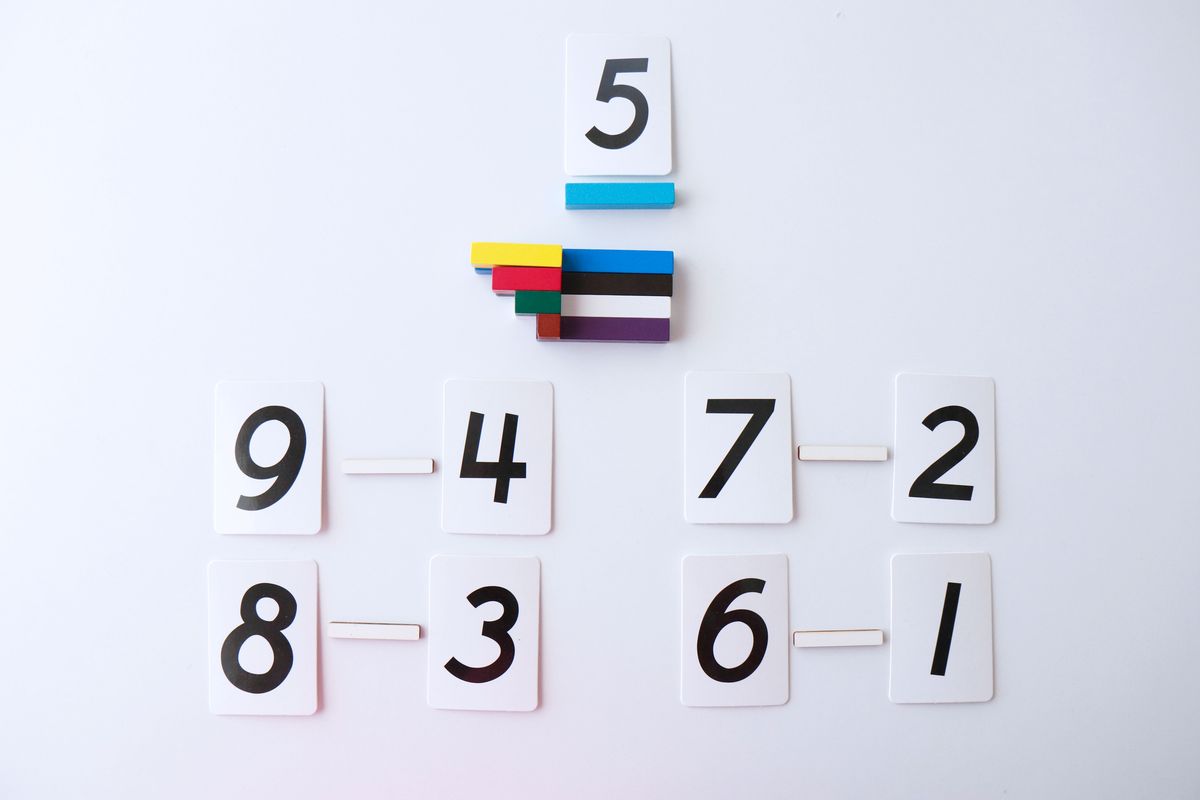
Descubrir el sustraendo
Del mismo modo que hemos visto antes en la suma, podemos descubrir el sustraendo de una resta.
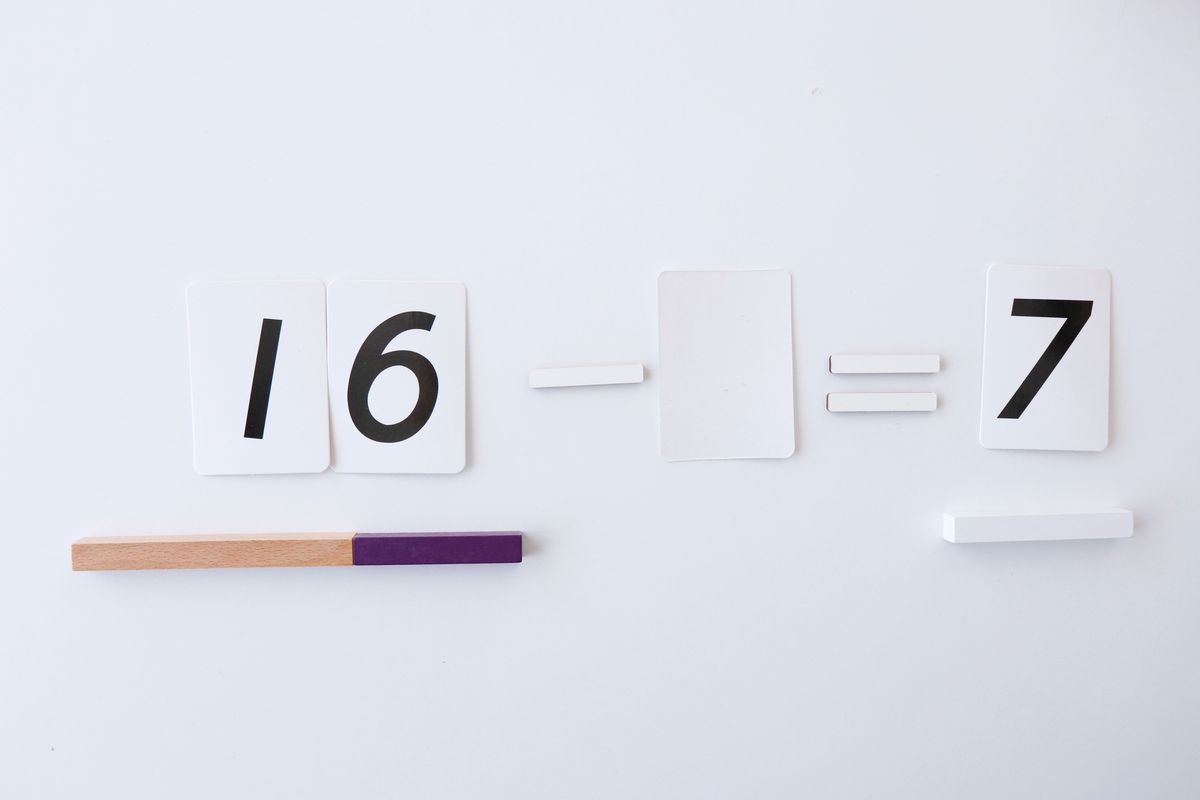

Par e impar
Es muy fácil representar y entender el concepto de par e impar con las regletas. Los números pares son aquellos que podemos descomponerlos en dos regletas iguales y los números impares son aquellos que no pueden descomponerse en dos regletas iguales.

Numeración decimal
Las regletas también nos servirán para la representación de números en base al sistema decimal, para ello podemos complementarlas con el set de base 10 Montessori que es del mismo color que nuestra regleta del número 10.

Con las regletas podemos representar los números desde el 11 hasta el 20 (y posteriores).

Si usamos el tapete que incluimos en el imprimible que os dejamos al final de este post, podemos representar números grandes e incluir las centenas y los millares de la base 10.

En un nivel de abstracción superior podemos representar las decenas, centenas y millares con las regletas, sabiendo que si están situados en el espacio de las decenas, centenas o millares están respresentando dicho valor posicional.

Operaciones con tapete de valor posicional
Con las regletas y el tapete de valor posicional para operaciones que os adjuntamos en el imprimible que os dejamos al final del post podemos realizar sumas y restas más grandes e incluso con llevadas.
Suma con llevada

Al sumar las unidades nos da 11 así que dejamos una unidad en la zona de las unidades y pasamos la decena a la zona de las decenas.

El resultado final serán 41.

Resta con llevada
Para la resta con llevada, explicaremos a través del ejemplo. En la resta 44-28, como no podemos quitar 8 unidades a las 4 que tenemos cogeremos una decena y la pasaremos a las unidades.

Ahora si que tenemos suficientes unidades para quitar las 8, colocamos la regleta del 8 al lado de las unidades que tenemos para averiguar qué número es el que nos queda.

Ahora si que podemos quitarle 8 y 6 son lo que nos queda.

Así que pasamos la regleta del 6 a la zona del resultado.

En las decenas vemos que tenemos que quitar 2 a las 3 que tenemos arriba, así que nos quedará 1.

Por tanto el resultado serán 16.

En este tipo de operaciones es interesante utilizar dos tamaños diferentes de tarjetas de madera, así podemos en la suma que estamos sumando dos cantidades que resultaran más pequeñas que el resultado, por eso usamos tarjetas pequeñas de madera en los sumandos y tarjetas grandes en el resultado. Al contrario que en la resta que usamos las tarjetas grandes en el minuendo y el sustraendo, y tarjetas pequeñas en el resultado, ya que el resultado de la resta siempre será menor que los otros dos números.
La multiplicación
Para multiplicar dos números lo haremos construyendo un rectángulo cuyos lados representan los dos factores. Por ejemplo, en esta multiplicación el rectángulo formado es de lado 5 (cogemos regletas de 5) y lado 4 (número de regletas que cogemos). El resultado será el área de este rectángulo.
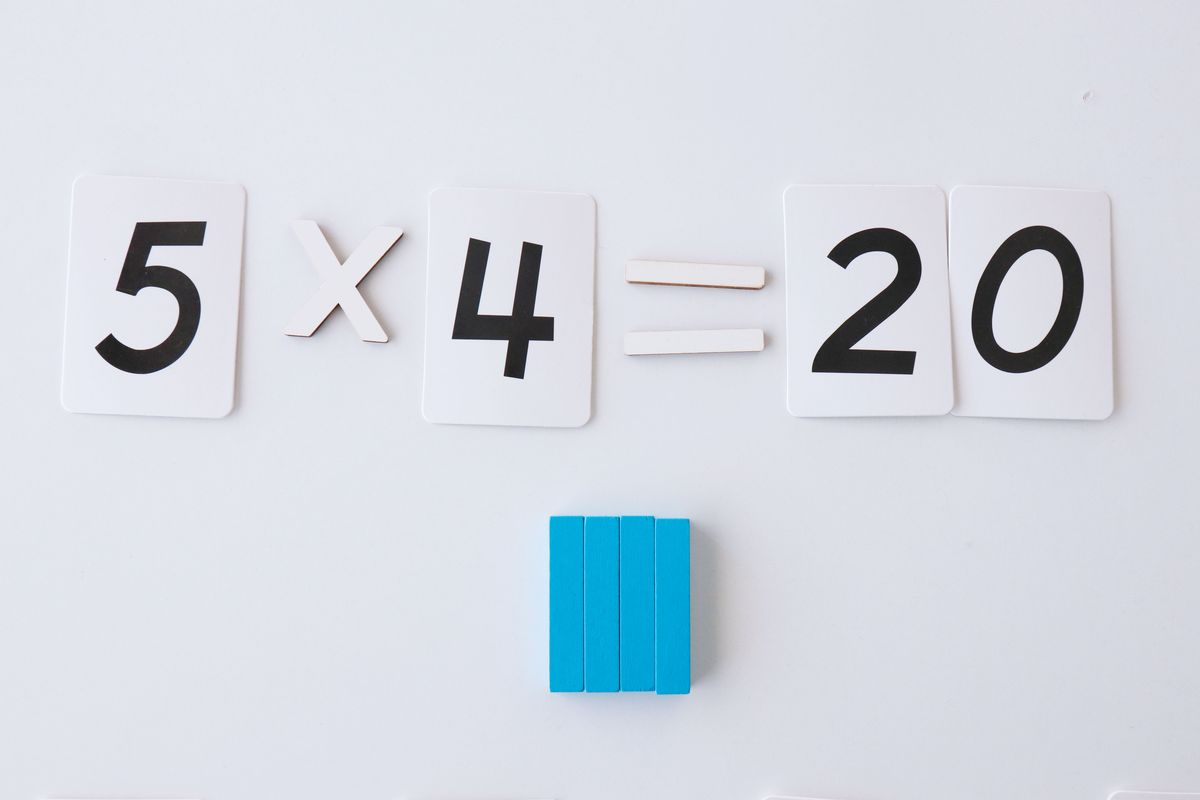
Podemos ver la multiplicación como una suma repetida de números y comprobarlo.
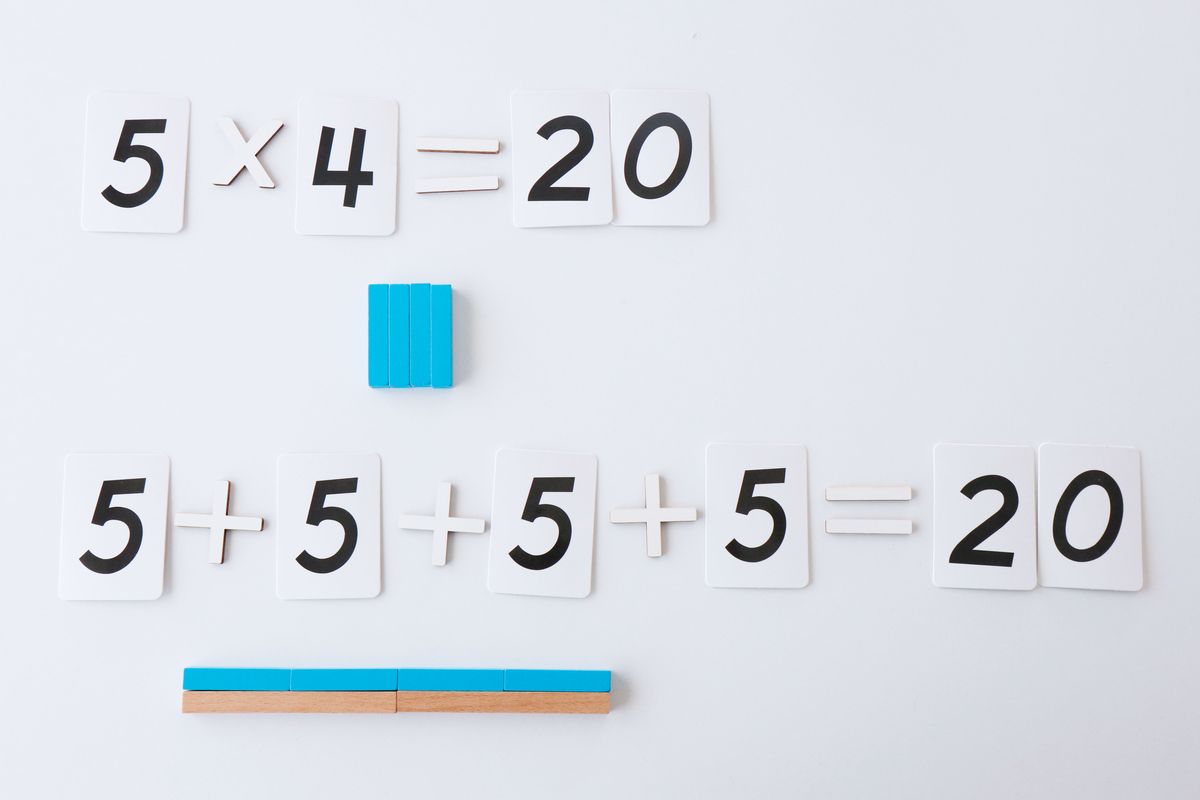
Para crear la multiplicación podemos crear un marco con los dos factores, así tendremos de referencia los dos lados que ha de tener el rectángulo. El resultado es el rectángulo formado en el interior del marco.


Multiplicación de tres factores
Para representar una multiplicación de tres factores hemos de tener en cuenta que multplicaremos dos de los factores y el resultado lo multplicaremos por el factor que faltaba.
Por ejemplo, aquí hemos multiplicado 4×5 y el resultado lo multiplicamos por 3.
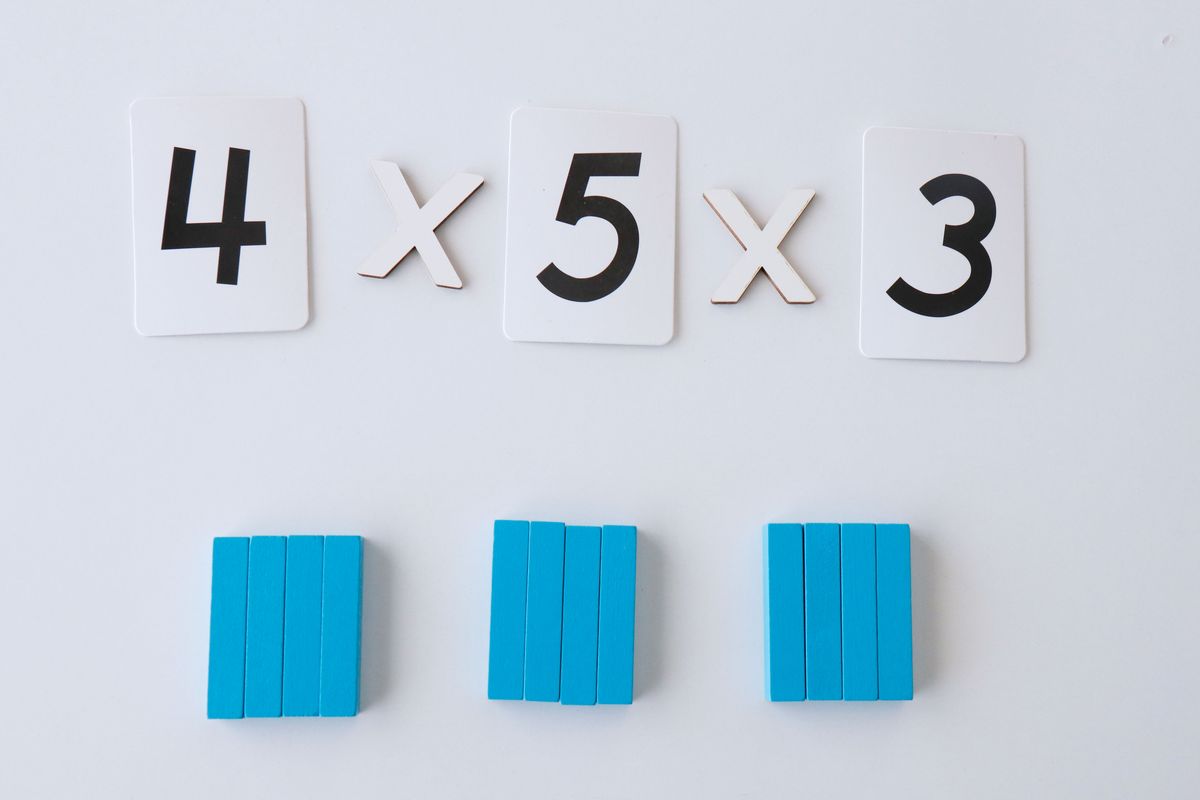
De esta manera se forma un prisma rectangular cuyo valor de sus aristas corresponden a los tres factores.

Propiedades de la multiplicación
Propiedad conmutativa
El orden de los factores no altera el producto. Podemos comprobar la propiedad conmutativa de la multiplicación con las regletas creando los dos rectángulos correspondientes de las dos multiplicaciones.
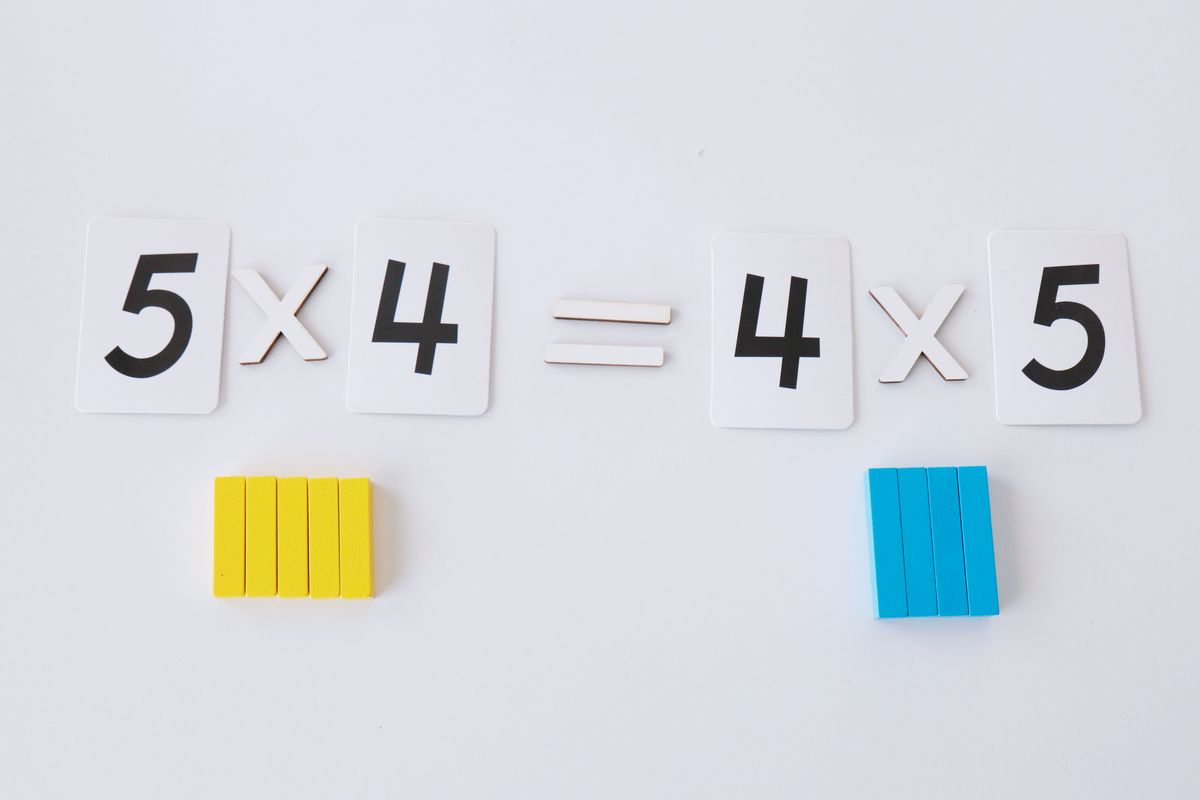
Para comprobar que el área del rectángulo es la misma situamos uno encima del otro.


Propiedad distributiva
La multiplicación de una suma es igual a la suma de las multiplicaciones de este número por cada sumando.
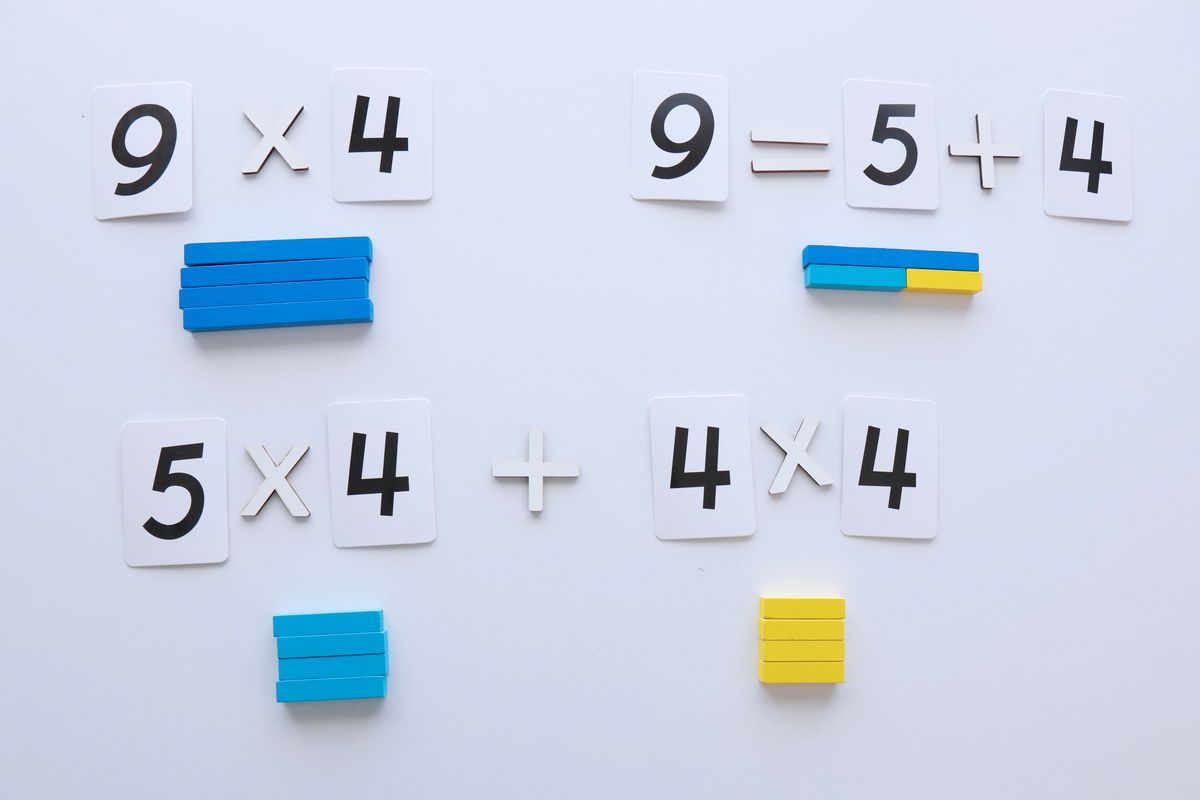
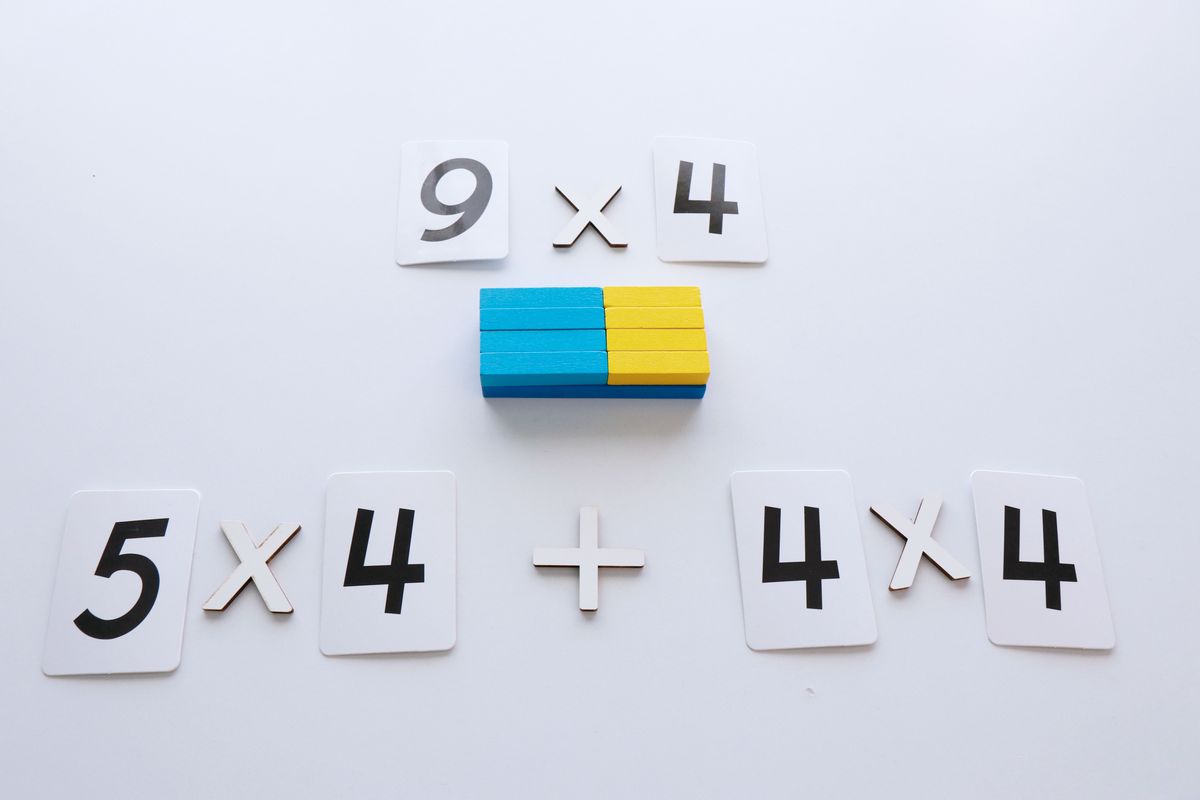
Propiedad asociativa
La forma de agrupar los factores no altera el resultado de la multiplicación. Así, cuando tenemos una multiplicación de 3 factores podemos agrupar cualquier de ellos y después multiplicar por el tercer factor. Por ejemplo en la multiplicación 4 x 5 x 3 podemos agrupar 4 x 5 y multiplicar el por 3 el resultado.

O multiplicar 5×3 y multiplicar por 4 el resultado.

En ambos casos el resultado son 60, formamos los prismas rectangulares cuyos lados y arista son 4, 5 y 3.

Aunque los dos prismas rectangulares sean diferentes podemos comprobar que su volumen es el mismo.

Doble, triple y mitad
Los conceptos de doble y triple son un acercamiento natural a la multiplicación. Para representarlo en las regletas solo tendremos que poner dos regletas iguales en el doble.


Para la mitad repartimos un número entre dos cantidades iguales.

Y para el triple multiplicamos la cantidad por 3.


Representación de las tablas de multiplicar
Podemos representar las tablas de multiplicar con las regletas y la caja de operaciones de la multiplicación.
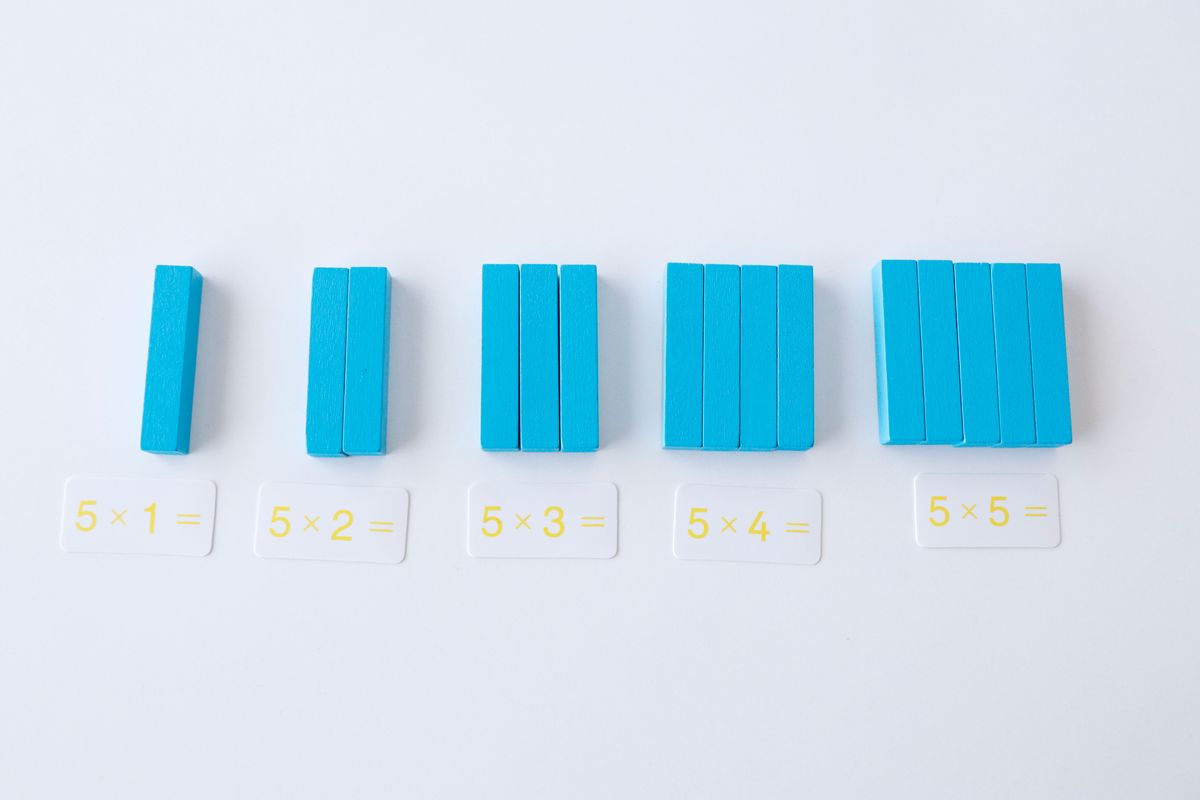
De esta forma, cuando llegamos a un cuadrado se aprecia que se forma un cuadrado con las regletas.

Aquí podemos ver los cuadrados de todos los números.

La tabla pitagórica o decanomio Montessori
La tabla de Pitágoras o decanomio Montessori es la representación de las 10 primeras tablas de multiplicar juntas. Esta representación presenta unas relaciones numéricas visuales muy curiosas e interesantes y si además respresentamos la Tabla Pitagórica con las regletas va a ser mucho más visual y manipulativo. El decanomio Montessori consiste en representar tanto con las regletas como con las perlas las tablas de multiplicar en un gráfico de doble entrada, donde ponemos las tablas ordenadas en los dos ejes.

Al respresentar todas las tablas de multiplicar en el decanomio o tabla de Pitágoras podemos ver curiosidades como que la diagonal de esta representación contiene los cuadrados de los números o que esta diagonal divide la tabla en dos mitades iguales.

Además, si ponemos todas las regletas sobre la diagonal se formarán los cubos de los números.



Esta presentación la podemos hacer también a nivel sensorial con la caja de la Tabla de Pitágoras. En este caso, se haría a modo de puzle sin operaciones numéricas.

Más adelante podemos ver estas relaciones numéricas tanto con la caja de perlas del decanomio Montessori como con las regletas.

Podemos ir etiquetando cada sección con las tarjetas de madera de la caja de multiplicaciones, así verbalizamos y representamos gráficamente.

La división con regletas
Para dividir con las regletas repartimos una cantidad entre un número de montones o peones. En este caso ponemos los muñecos de Grimm’s para hacer la repartición.

Para repartir la cantidad tendremos que cambiar las regletas por un número de regletas igual a los peones a los que tenemos que repartir.

El resultado de la división es lo que consigue uno de los peones. En este caso son 4, por que las regletas son de 4.

Si la división no es exacta hacemos la repartición y dejamos lo que sobra como resto.
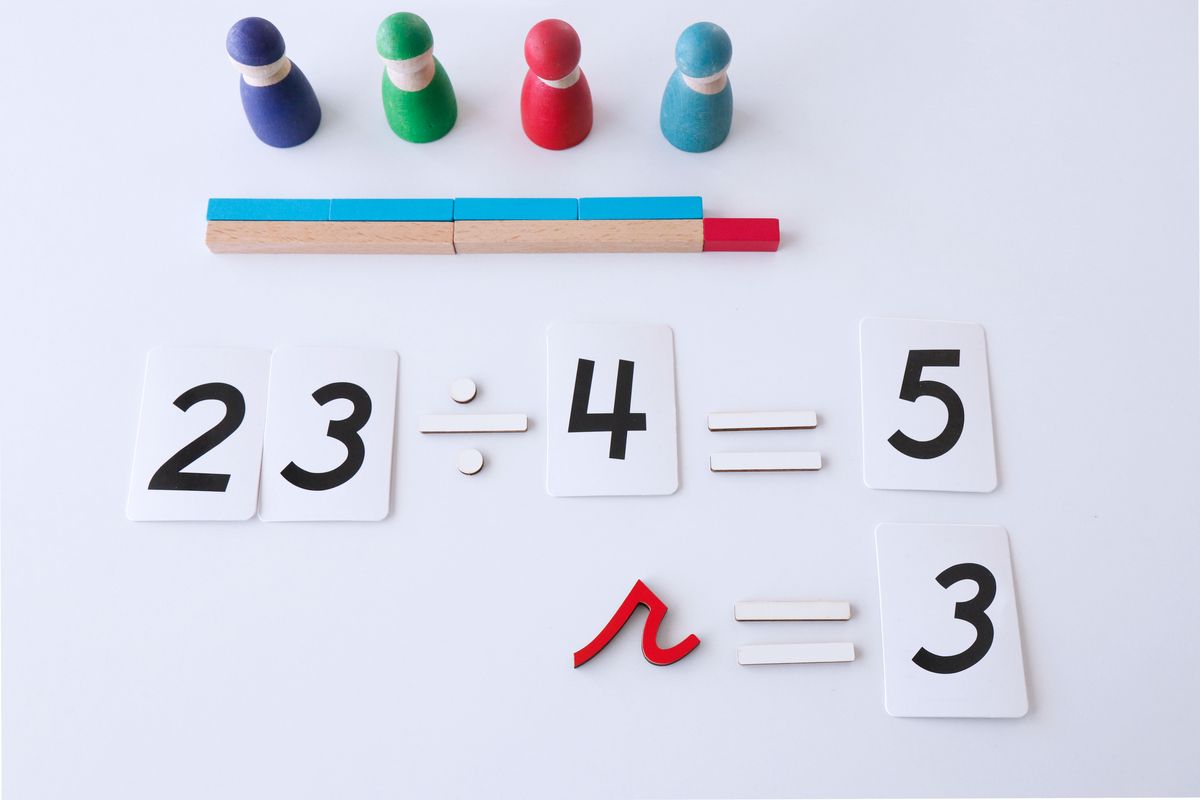
La multiplicación y división como operaciones inversas
Podemos respresentar con las regletas la multiplicación y división como operaciones inversas y ver de forma manipulativa esta relación.
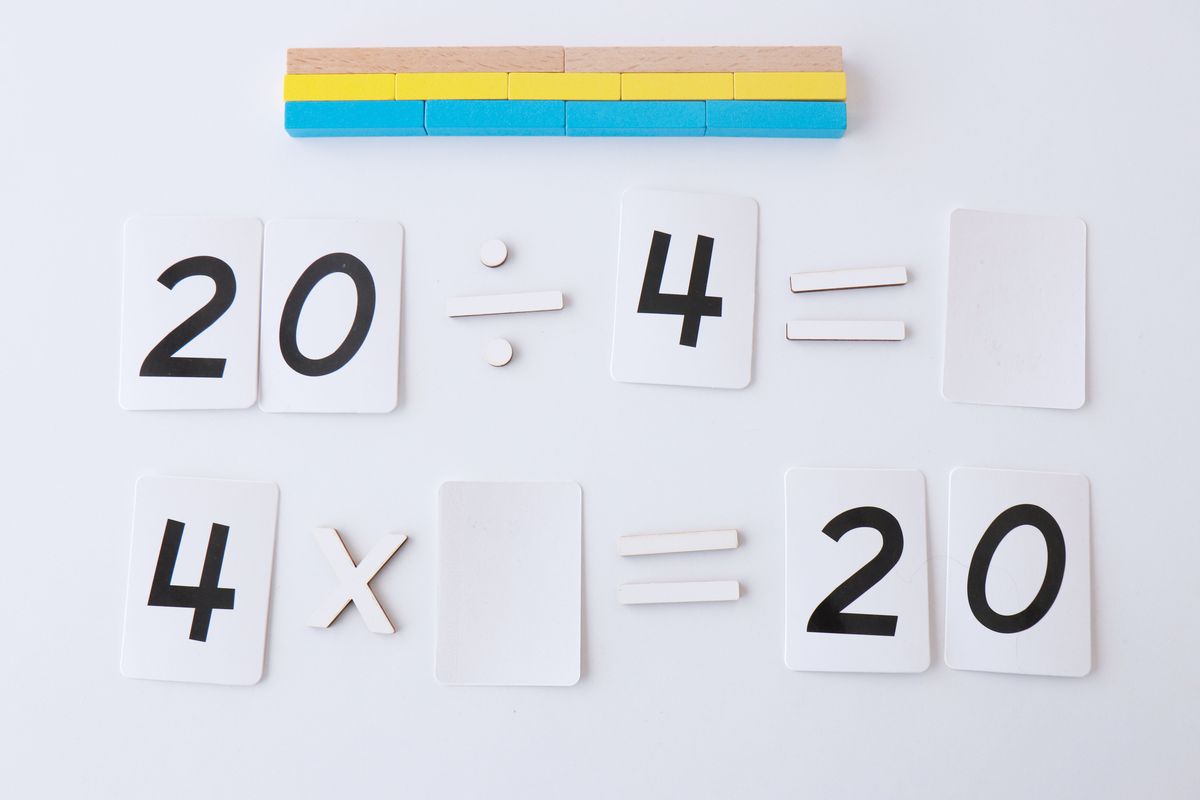
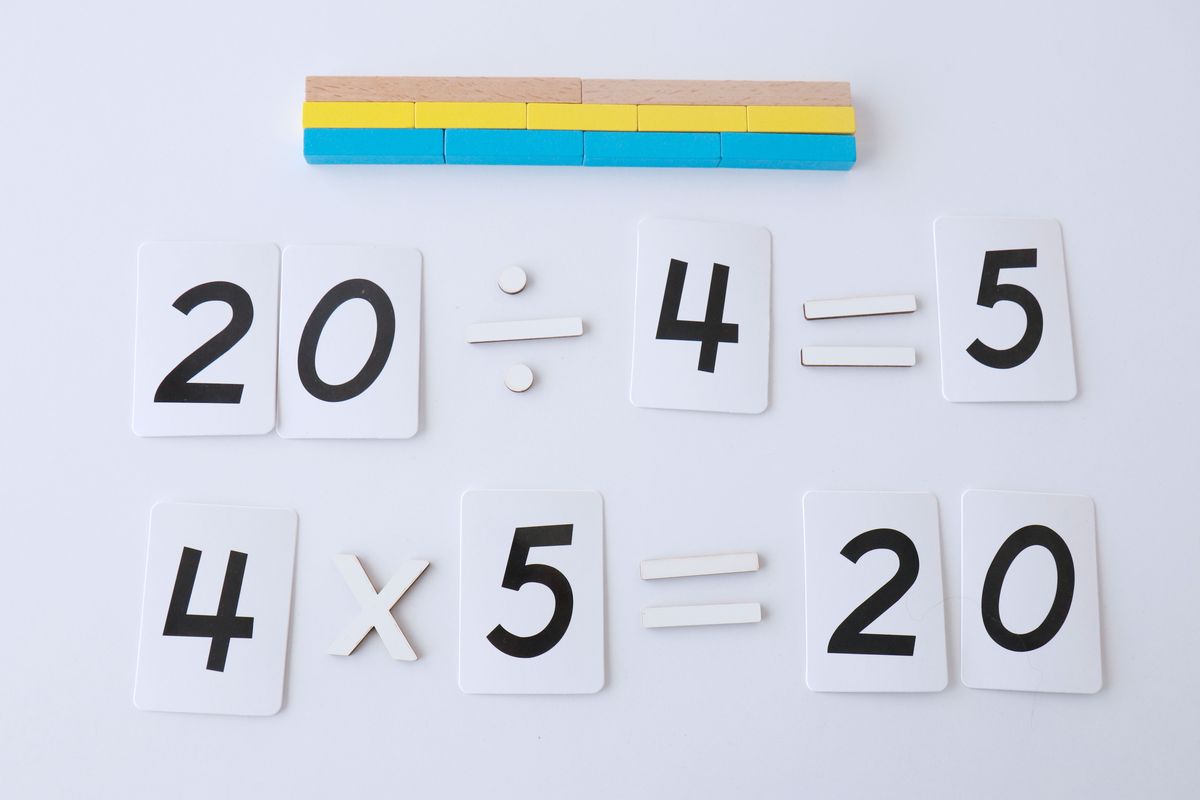
La media aritmética con regletas
Otro concepto muy interesante a partir de la investigación con las regletas es la media aritmética.
La media aritmética es el valor resultante de sumar ciertas cantidades y dividir el resultando por el número de cantidades que teníamos. Podemos representarlo de la siguiente forma con las regletas. Tenemos los siguientes números: 3, 6, 9 y 10. Colocamos las regletas de cada uno de ellos y los sumamos. Al hacer la suma la representamos con el menor número de regletas posible, como en este caso es 28 ponemos dos regletas de 10 y uno de 8. Después intentamos conseguir un número de regletas iguales que nos permitan completar el espacio de 28.

Después de varios intentos podemos ver que podemos hacer 28 con regletas de 7, así que la media aritmética de 3, 6, 9 y 10 es 7.

Una vez llegado a este punto en nuestra investigación podemos pensar qué operaciones son las que hemos hecho manipulando las regletas, para generalizar sobre la fórmula. De esta forma sabremos la razón de ella y comprenderemos el porqué.

La raíz cuadrada con regletas
La raíz cuadrada de un número se trata de averiguar el número del que se conoce su cuadrado.
Para su representación en regletas trataremos de formar con regletas de uno un cuadrado exacto. Por ejemplo, para saber la raíz cuadrada de 20 cogemos 20 regletas de 1 y tratamos de hacer con ellas un cuadrado.

Para ello empezamos haciendo un cuadrado pequeñito de 4 regletas y lo vamos aumentando por los lados.


A medida que lo vamos formando vemos que nos van a sobrar regletas porque no tenemos suficientes para formar un cuadrado más grande, así que habrá resto.

Finalmente el resultado será el número del lado de este cuadrado que hemos formado y el resto los cuadraditos que nos han sobrado. Así la raíz cuadrada de 20 será 4 con resto 4. Este es un concepto que les resulta muy abstracto a los niños pero que hecho de esta forma se entiende perfectamente.

Perímetro
Podemos calcular el perímetro de una figura geométrica con las regletas sumando el valor de las regletas que cubren este perímetro.

Descargar imprimible para las regletas Montessori
¿Dónde comprar material de matemáticas Montessori?
En nuestra tienda online puedes encontrar una gran variedad de material de matemáticas de la metodología Montessori, como las perlas y las regletas, así como el resto de materiales mostrados en este post, entre muchos otros.

Ver material de matemáticas Montessori en nuestra tienda online







Pingback: IDEAS PARA APRENDER LOS NÚMEROS CON MATERIALES DE GRIMM’S – El Blog de Juguete
mirey
yo quise mas jugretes para mi niña ari
Sonia
Hola, soy maestra y me encanta vuestra tienda, pero tengo que discrepar en algo de lo que decís sobre las regletas Cuisenaire: los colores, aunque lo parezca, no son aleatorios, sino que tienen su lógica en las relaciones numéricas que los niños y niñas encontrarán jugando con las regletas. Según Cuisenaire, la roja (2) y la rosa (4) y la marrón (8) forman una familia, la verde clara (3), la verde oscura (6) y la azul (9) otra, la amarilla (5) y la naranja (10) otra. La negra (7) va sola como número primo que es, y la blanca (1) es la unidad. Así que los colores, en las regletas Cuisenaire, no están por mera estética ni son aleatorios. Espero haber ayudado. Un saludo.